Определение центра окружности, описанной вокруг треугольника, является важной задачей в геометрии. Геометрический центр фигуры является точкой, которая находится на равном расстоянии от всех ее точек. В случае треугольника, центр окружности, описанной вокруг него, является точкой пересечения перпендикуляров, проведенных из середин каждой стороны треугольника. Это понимание поможет вам лучше понять свойства и структуру этой фигуры, а также сможет быть использовано для решения различных задач в геометрии.
Введение
Центр описанной около треугольника окружности – это один из важных элементов геометрии, который играет важную роль в решении различных задач. В этой статье мы рассмотрим определение центра описанной около треугольника окружности, ее свойства, преимущества и недостатки.
Определение
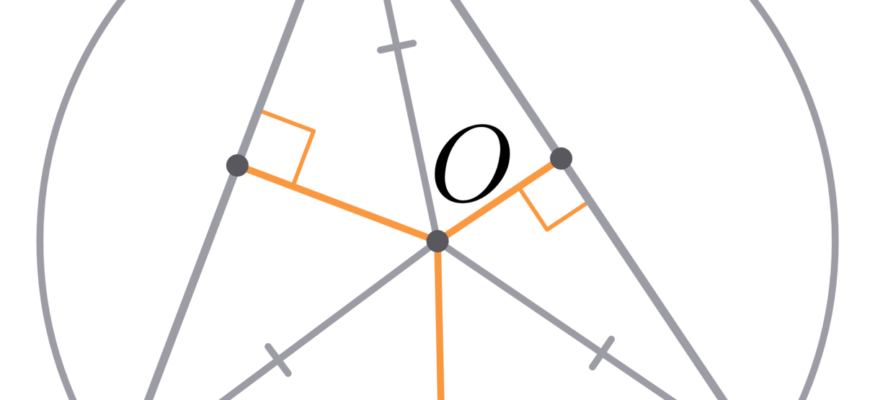
Центр описанной около треугольника окружности – это точка пересечения перпендикуляров, опущенных из середин сторон треугольника на противолежащие стороны.
Свойства
Центр описанной около треугольника окружности имеет следующие свойства:
— От центра описанной около треугольника окружности до вершин треугольника расстояния равны.
— Любая сторона треугольника является диаметром окружности, описанной вокруг треугольника.
— Угол, образованный хордой и дугой, равен половине центрального угла, соответствующего этой дуге.
— Центр описанной около треугольника окружности лежит на пересечении биссектрис треугольника.
Преимущества и недостатки
Преимущества использования центра описанной около треугольника окружности заключаются в том, что это позволяет более легко решать задачи, связанные с геометрией, такие как определение площади треугольника, его высоты, медианы и т.д.
Недостатки использования центра описанной около треугольника окружности заключаются в сложности в расчетах и использовании в реальных ситуациях.
Список
Приведем список задач, в которых центр описанной около треугольника окружности играет важную роль:
— Определение площади треугольника
— Определение его высоты, медианы и биссектрисы
— Решение задач на построение треугольника
— Расчет расстояния между точками
FAQ
1. Как найти центр описанной около треугольника окружности?
Для нахождения центра описанной около треугольника окружности необходимо опустить перпендикуляры из середин сторон треугольника на противолежащие стороны. Точка пересечения этих перпендикуляров является центром описанной около треугольника окружности.
2. Какие свойства имеет центр описанной около треугольника окружности?
Центр описанной около треугольника окружности имеет следующие свойства: расстояние от центра до вершин треугольника равны, любая сторона треугольника является диаметром окружности, описанной вокруг треугольника, угол, образованный хордой и дугой, равен половине центрального угла, соответствующего этой дуге, и центр описанной около треугольника окружности лежит на пересечении биссектрис треугольника.
3. В каких задачах центр описанной около треугольника окружности играет важную роль?
Центр описанной около треугольника окружности играет важную роль в задачах на определение площади треугольника, его высоты, медианы и биссектрисы, в задачах на построение треугольника и в расчете расстояния между точками.
Читайте далее: